Home  ›  Cs188 Solutions Naive Bayes Your Friend Claims That He Can Write an Effective Naive Bayes

Cs188 Solutions Naive Bayes Your Friend Claims That He Can Write an Effective Naive Bayes

Written By Sunday, 12 December 2021 Add Comment Edit

Homework 5: Classification

The Pacman AI projects were developed at UC Berkeley, primarily by John DeNero (denero@cs.berkeley.edu) and Dan Klein (klein@cs.berkeley.edu). For more info, see http://inst.eecs.berkeley.edu/~cs188/sp09/pacman.html

Introduction

In this project, you will design three classifiers: a naive Bayes classifier, a perceptron classifier and a large-margin (MIRA) classifier. You will test your classifiers on two image data sets: a set of scanned handwritten digit images and a set of face images in which edges have already been detected. Even with simple features, your classifiers will be able to do quite well on these tasks when given enough training data.

Optical character recognition (OCR) is the task of extracting text from image sources. The first data set on which you will run your classifiers is a collection of handwritten numerical digits (0-9). This is a very commercially useful technology, similar to the technique used by the US post office to route mail by zip codes. There are systems that can perform with over 99% classification accuracy (see LeNet-5 for an example system in action).

Face detection is the task of localizing faces within video or still images. The faces can be at any location and vary in size. There are many applications for face detection, including human computer interaction and surveillance. You will attempt a simplified face detection task in which your system is presented with an image that has been pre-processed by an edge detection algorithm. The task is to determine whether the edge image is a face or not. There are several systems in use that perform quite well at the face detection task. One good system is the Face Detector by Schneiderman and Kanade.

The code for this project includes the following files and data, available as a zip file.

Data file
data.zip Data file, including the digit and face data.
Files you will edit
naiveBayes.py The location where you will write your naive Bayes classifier.
perceptron.py The location where you will write your perceptron classifier.
mira.py The location where you will write your MIRA classifier.
dataClassifier.py The wrapper code that will call your classifiers. You will also write your enhanced feature extractor here. You will also use this code to analyze the behavior of your classifier.
answers.py Answers to Question 2 and Question 4 go here.
Files you should read but NOT edit
classificationMethod.py Abstract super class for the classifiers you will write.
(You should read this file carefully to see how the infrastructure is set up.)
samples.py I/O code to read in the classification data.
util.py Code defining some useful tools. You may be familiar with some of these by now, and they will save you a lot of time.
mostFrequent.py A simple baseline classifier that just labels every instance as the most frequent class.

What to submit: You will fill in portions of naiveBayes.py, perceptron.py, mira.py, dataClassifier.py and answers.py (only) during the assignment, and submit them.

Evaluation: Your code will be autograded for technical correctness. Please do not change the names of any provided functions or classes within the code, or you will wreak havoc on the autograder.

Academic Dishonesty: We will be checking your code against other submissions in the class for logical redundancy. If you copy someone else's code and submit it with minor changes, we will know. These cheat detectors are quite hard to fool, so please don't try. We trust you all to submit your own work only; please don't let us down. Instead, contact the course staff if you are having trouble.

Getting Started

To try out the classification pipeline, run dataClassifier.py from the command line. This will classify the digit data using the default classifier (mostFrequent) which blindly classifies every example with the most frequent label. 

python dataClassifier.py

As usual, you can learn more about the possible command line options by running: 

python dataClassifier.py -h

We have defined some simple features for you. Later you will design some better features. Our simple feature set includes one feature for each pixel location, which can take values 0 or 1 (off or on). The features are encoded as a Counter where keys are feature locations (represented as (column,row)) and values are 0 or 1. The face recognition data set has value 1 only for those pixels identified by a Canny edge detector.

Implementation Note: You'll find it easiest to hard-code the binary feature assumption. If you do, make sure you don't include any non-binary features. Or, you can write your code more generally, to handle arbitrary feature values, though this will probably involve a preliminary pass through the training set to find all possible feature values (and you'll need an "unknown" option in case you encounter a value in the test data you never saw during training).

Naive Bayes

A skeleton implementation of a naive Bayes classifier is provided for you in naiveBayes.py. You will fill in the trainAndTune function, the calculateLogJointProbabilities function and the findHighOddsFeatures function.

Theory

A naive Bayes classifier models a joint distribution over a label $Y$ and a set of observed random variables, or features, $\{F_1, F_2, \ldots F_n\}$, using the assumption that the full joint distribution can be factored as follows (features are conditionally independent given the label):

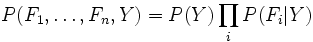
\begin{displaymath} P(F_1 \ldots F_n, Y) = P(Y) \prod_i P(F_i \vert Y) \end{displaymath}

To classify a datum, we can find the most probable label given the feature values for each pixel, using Bayes theorem:

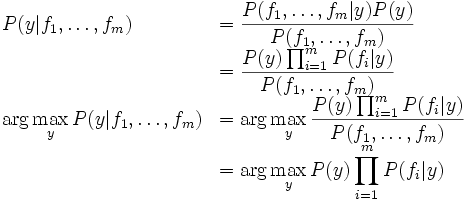
\begin{eqnarray*} P(y \vert f_1, \ldots, f_m) &=& \frac{P(f_1, \ldots, f_m \... ... &=& \textmd{arg max}_{y} P(y) \prod_{i = 1}^m P(f_i \vert y) \end{eqnarray*}

Because multiplying many probabilities together often results in underflow, we will instead compute log probabilities which have the same argmax:

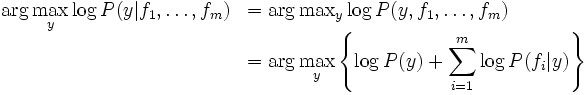
\begin{eqnarray*} \textmd{arg max}_{y} log(P(y \vert f_1, \ldots, f_m) &=& \te... ...{arg max}_{y} (log(P(y)) + \sum_{i = 1}^m log(P(f_i \vert y))) \end{eqnarray*}

To compute logarithms, use math.log(), a built-in Python function.

Parameter Estimation

Our naive Bayes model has several parameters to estimate. One parameter is the prior distribution over labels (digits, or face/not-face), $P(Y)$.

We can estimate $P(Y)$ directly from the training data:

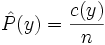
\begin{displaymath} \hat{P}(y) = \frac{c(y)}{n} \end{displaymath}


where $c(y)$ is the number of training instances with label y and n is the total number of training instances.

The other parameters to estimate are the conditional probabilities of our features given each label y: $P(F_i \vert Y = y)$. We do this for each possible feature value ($f_i \in {0,1}$).

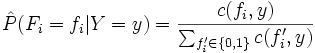
\begin{eqnarray*} \hat{P}(F_i=f_i\vert Y=y) &=& \frac{c(f_i,y)}{\sum_{f_i}{c(f_i,y)}} \\ \end{eqnarray*}


where $c(f_i,y)$ is the number of times pixel $F_i$ took value $f_i$ in the training examples of label y.

Smoothing

Your current parameter estimates are unsmoothed, that is, you are using the empirical estimates for the parameters $P(f_i\vert y)$. These estimates are rarely adequate in real systems. Minimally, we need to make sure that no parameter ever receives an estimate of zero, but good smoothing can boost accuracy quite a bit by reducing overfitting.

In this project, we use Laplace smoothing, which adds k counts to every possible observation value:

$P(F_i=f_i\vert Y=y) = \frac{c(F_i=f_i,Y=y)+k}{\sum_{f_i}{(c(F_i=f_i,Y=y)+k)}}$

If k=0, the probabilities are unsmoothed. As k grows larger, the probabilities are smoothed more and more. You can use your validation set to determine a good value for k. Note: don't smooth P(Y).

Question 1 (6 points) Implement trainAndTune and calculateLogJointProbabilities in naiveBayes.py. In trainAndTune, estimate conditional probabilities from the training data for each possible value of k given in the list kgrid. Evaluate accuracy on the held-out validation set for each k and choose the value with the highest validation accuracy. In case of ties, prefer the lowest value of k. Test your classifier with: 

python dataClassifier.py -c naiveBayes --autotune

Hints and observations:

  • The method calculateLogJointProbabilities uses the conditional probability tables constructed by trainAndTune to compute the log posterior probability for each label y given a feature vector. The comments of the method describe the data structures of the input and output.
  • You can add code to the analysis method in dataClassifier.py to explore the mistakes that your classifier is making. This is optional.
  • When trying different values of the smoothing parameter k, think about the number of times you scan the training data. Your code should save computation by avoiding redundant reading.
  • To run your classifier with only one particular value of k, remove the --autotune option. This will ensure that kgrid has only one value, which you can change with -k.
  • Using a fixed value of k=2 and 100 training examples, you should get a validation accuracy of about 69% and a test accuracy of 55%.
  • Using --autotune, which tries different values of k, you should get a validation accuracy of about 74% and a test accuracy of 65%.
  • Accuracies may vary slightly because of implementation details. For instance, ties are not deterministically broken in the Counter.argMax() method.
  • To run on the face recognition dataset, use -d faces (optional).

Odds Ratios

One important tool in using classifiers in real domains is being able to inspect what they have learned. One way to inspect a naive Bayes model is to look at the most likely features for a given label.

Another, better, tool for understanding the parameters is to look at odds ratios. For each pixel feature $F_i$ and classes $y_1, y_2$, consider the odds ratio:

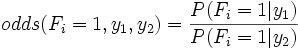
\begin{displaymath} \mbox{odds}(F_i=on, y_1, y_2) = \frac{P(F_i=on\vert y_1)}{P(F_i=on\vert y_2)} \end{displaymath}


This ratio will be greater than one for features which cause belief in $y_1$ to increase relative to $y_2$.

The features that have the greatest impact at classification time are those with both a high probability (because they appear often in the data) and a high odds ratio (because they strongly bias one label versus another).

Question 2 (2 points) Fill in the function findHighOddsFeatures(self, label1, label2). It should return a list of the 100 features with highest odds ratios for label1 over label2. The option -o activates an odds ratio analysis. Use the options -1 label1 -2 label2 to specify which labels to compare. Running the following command will show you the 100 pixels that best distinguish between a 3 and a 6. 

python dataClassifier.py -a -d digits -c naiveBayes -o -1 3 -2 6
Use what you learn from running this command to answer the following question. Which of the following images best shows those pixels which have a high odds ratio with respect to 3 over 6? (That is, which of these is most like the output from the command you just ran?)
(a)
(b)
(c)
(d)
(e)
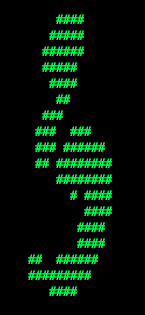To answer: please return 'a', 'b', 'c', 'd', or 'e' from the function q2 in answers.py. Note: this part of the question will not be autograded.

Perceptron


A skeleton implementation of a perceptron classifier is provided for you in perceptron.py. You will fill in the train function, and the findHighWeightFeatures function.

Unlike the naive Bayes classifier, a perceptron does not use probabilities to make its decisions. Instead, it keeps a weight vector $w^y$ of each class $y$ ($y$ is an identifier, not an exponent). Given a feature list $f$, the perceptron compute the class $y$ whose weight vector is most similar to the input vector $f$. Formally, given a feature vector $f$ (in our case, a map from pixel locations to indicators of whether they are on), we score each class with:

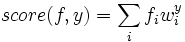
\begin{displaymath} \mbox{score}(f,y) = \sum_i f_i w^y_i \end{displaymath}

Then we choose the class with highest score as the predicted label for that data instance. In the code, we will represent $w^y$ as a Counter.

Learning weights

In the basic multi-class perceptron, we scan over the data, one instance at a time. When we come to an instance 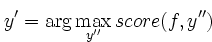$(f, y)$, we find the label with highest score:

\begin{displaymath} y' = \textmd{arg max}_{y''} score(f,y'') \end{displaymath}

We compare $y'$ to the true label $y$. If $y' = y$, we've gotten the instance correct, and we do nothing. Otherwise, we guessed $y'$ but we should have guessed $y$. That means that $w^y$ should have scored $f$ higher, and $w^{y'}$ should have scored $f$ lower, in order to prevent this error in the future. We update these two weight vectors accordingly:

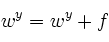
\begin{displaymath} w^y += f \end{displaymath}

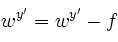
\begin{displaymath} w^{y'} -= f \end{displaymath}

Using the addition, subtraction, and multiplication functionality of the Counter class in util.py, the perceptron updates should be relatively easy to code. Certain implementation issues have been taken care of for you in perceptron.py, such as handling iterations over the training data and ordering the update trials. Furthermore, the code sets up the weights data structure for you. Each legal label needs its own Counter full of weights.

Question 3 (4 points) Fill in the train method in perceptron.py. Run your code with: 

python dataClassifier.py -c perceptron

Hints and observations:

  • The command above should yield validation accuracies in the range between 40% to 70% and test accuracy between 40% and 70% (with the default 3 iterations). These ranges are wide because the perceptron is a lot more sensitive to the specific choice of tie-breaking than naive Bayes.
  • One of the problems with the perceptron is that its performance is sensitive to several practical details, such as how many iterations you train it for, and the order you use for the training examples (in practice, using a randomized order works better than a fixed order). The current code uses a default value of 3 training iterations. You can change the number of iterations for the perceptron with the -i iterations option. Try different numbers of iterations and see how it influences the performance. In practice, you would use the performance on the validation set to figure out when to stop training, but you don't need to implement this stopping criterion for this assignment.

Visualizing weights

Perceptron classifiers, and other discriminative methods, are often criticized because the parameters they learn are hard to interpret. To see a demonstration of this issue, we can write a function to find features that are characteristic of one class. (Note that, because of the way perceptrons are trained, it is not as crucial to find odds ratios.)

Question 4 (1 point) Fill in findHighWeightFeatures(self, label) in perceptron.py. It should return a list of the 100 features with highest weight for that label. You can display the 100 pixels with the largest weights using the command: 

python dataClassifier.py -c perceptron -w
Use this command to look at the weights, and answer the following true/false question. Which of the following sequence of weights is most representative of the perceptron?
(a)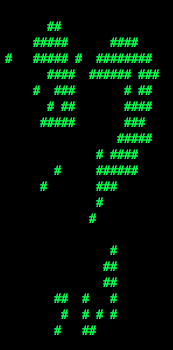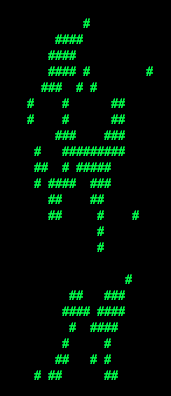
(b)
Answer the question answers.py in the method q4, returning either 'a' or 'b'. Note: the autograder will not grade this question.

MIRA

A skeleton implementation of the MIRA classifier is provided for you in mira.py. MIRA is an online learner which is closely related to both the support vector machine and perceptron classifiers. You will fill in the trainAndTune function.

Theory

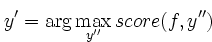
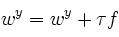
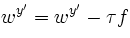
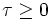Similar to a multi-class perceptron classifier, multi-class MIRA classifier also keeps a weight vector $w^y$ of each label $y$. We also scan over the data, one instance at a time. When we come to an instance $(f, y)$, we find the label with highest score:

We compare $y'$ to the true label $y$. If $y' = y$, we've gotten the instance correct, and we do nothing. Otherwise, we guessed $y'$ but we should have guessed $y$. Unlike perceptron, we update the weight vectors of these labels with variable step size:

where is chosen such that it minimizes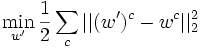

subject to the condition that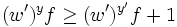


which is equivalent to

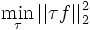subject to 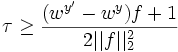and

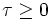
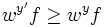Note that, , so the condition 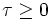is always true given 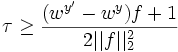Solving this simple problem, we then have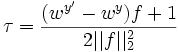

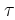However, we would like to cap the maximum possible value of by a positive constant C, which leads us to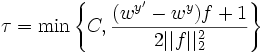


Question 5 (6 points) Implement trainAndTune in mira.py. This method should train a MIRA classifier using each value of C in Cgrid. Evaluate accuracy on the held-out validation set for each C and choose the C with the highest validation accuracy. In case of ties, prefer the lowest value of C. Test your MIRA implementation with: 
python dataClassifier.py -c mira --autotune

Hints and observations:

  • Pass through the data self.max_iterations times during training.
  • Store the weights learned using the best value of C at the end in self.weights, so that these weights can be used to test your classifier.
  • To use a fixed value of C=0.001, remove the --autotune option from the command above.
  • Validation and test accuracy when using --autotune should be in the 60's.
  • It might save some debugging time if the +1 term above is implemented as +1.0, due to division truncation of integer arguments. Depending on how you implement this, it may not matter.
  • The same code for returning high odds features in your perceptron implementation should also work for MIRA if you're curious what your classifier is learning.

Feature Design

Building classifiers is only a small part of getting a good system working for a task. Indeed, the main difference between a good classification system and a bad one is usually not the classifier itself (e.g. perceptron vs. naive Bayes), but rather the quality of the features used. So far, we have used the simplest possible features: the identity of each pixel (being on/off).

To increase your classifier's accuracy further, you will need to extract more useful features from the data. The EnhancedFeatureExtractorDigit in dataClassifier.py is your new playground. When analyzing your classifiers' results, you should look at some of your errors and look for characteristics of the input that would give the classifier useful information about the label. You can add code to the analysis function in dataClassifier.py to inspect what your classifier is doing. For instance in the digit data, consider the number of separate, connected regions of white pixels, which varies by digit type. 1, 2, 3, 5, 7 tend to have one contiguous region of white space while the loops in 6, 8, 9 create more. The number of white regions in a 4 depends on the writer. This is an example of a feature that is not directly available to the classifier from the per-pixel information. If your feature extractor adds new features that encode these properties, the classifier will be able exploit them. Note that some features may require non-trivial computation to extract, so write efficient and correct code.

Question 6 (6 points) Add new features for the digit dataset in the EnhancedFeatureExtractorDigit function in such a way that it works with your implementation of the naive Bayes classifier: this means that for this part, you are restricted to features which can take a finite number of discrete values (and if you have assumed that features are binary valued, then you are restricted to binary features). Note that you can encode a feature which takes 3 values [1,2,3] by using 3 binary features, of which only one is on at the time, to indicate which of the three possibilities you have. In theory, features aren't conditionally independent as naive Bayes requires, but your classifier can still work well in practice. We will test your classifier with the following command: 

python dataClassifier.py -d digits -c naiveBayes -f -a -t 1000
With the basic features (without the -f option), your optimal choice of smoothing parameter should yield 82% on the validation set with a test performance of 79%. You will receive 3 points for implementing new feature(s) which yield any improvement at all. You will receive 3 additional points if your new feature(s) give you a test performance greater than or equal to 84% with the above command.

Congratulations! You're finished with the CS 188 projects.

Cs188 Solutions Naive Bayes Your Friend Claims That He Can Write an Effective Naive Bayes

Source: https://www.ccs.neu.edu/home/rplatt/cs5100_2013/homework5/classification/classification.html

0 Response to "Cs188 Solutions Naive Bayes Your Friend Claims That He Can Write an Effective Naive Bayes"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel